Cum sa bati pe oricine la "Piatra, hartie, foarfeca". Iata tactica perfecta
Jocul a fost studiat in detaliu. Iata ce s-a descoperit
Jocul "Piatra, hartie, foarfeca", cunoscut sub numele de jan-ken-pon in japoneza, rochambeau in franceza si Rock-Paper-Scissor in engleza, este extrem de popular si un joc ce este studiat de mult timp de matematicieni si teoriticieni ai jocurilor.
Iar un nou experiment efectuat de Zhijian Wang la Universitatea Zhejiang din China ar putea sa dezvaluie solutia pentru a castiga de cele mai multe ori in fata adversarilor.
In cadrul acestui experiment, Zhijian a observat ca jucatorii castigatori obisnuiesc sa-si pastreze strategia invingatoare, in timp ce cei care pierd au tendinta de a o schimba in secventa, urmand ceea ce Zhijian numeste "persistent cyclic flows".
Iata cum functioneaza in practica: jucatorul A si jucatorul B incep amandoi folosind strategii aleatorii. Daca jucatorul A alege piata si Jucatorul B alege hartia, Jucatorul A pierde. In runda urmatoare, jucatorul A poate presupune ca jucatorul B va folosi din nou hartia si atunci foloseste foarfeca pentru a castiga. In runda urmatoare, pentru ca jucatorul B a pierdut, jucatorul A poate presupune ca jucatorul B va folosi urmatoarea strategie din secventa, foarfeca, si jucatorul A ar trebui sa foloseasca atunci piatra, castigand din nou.
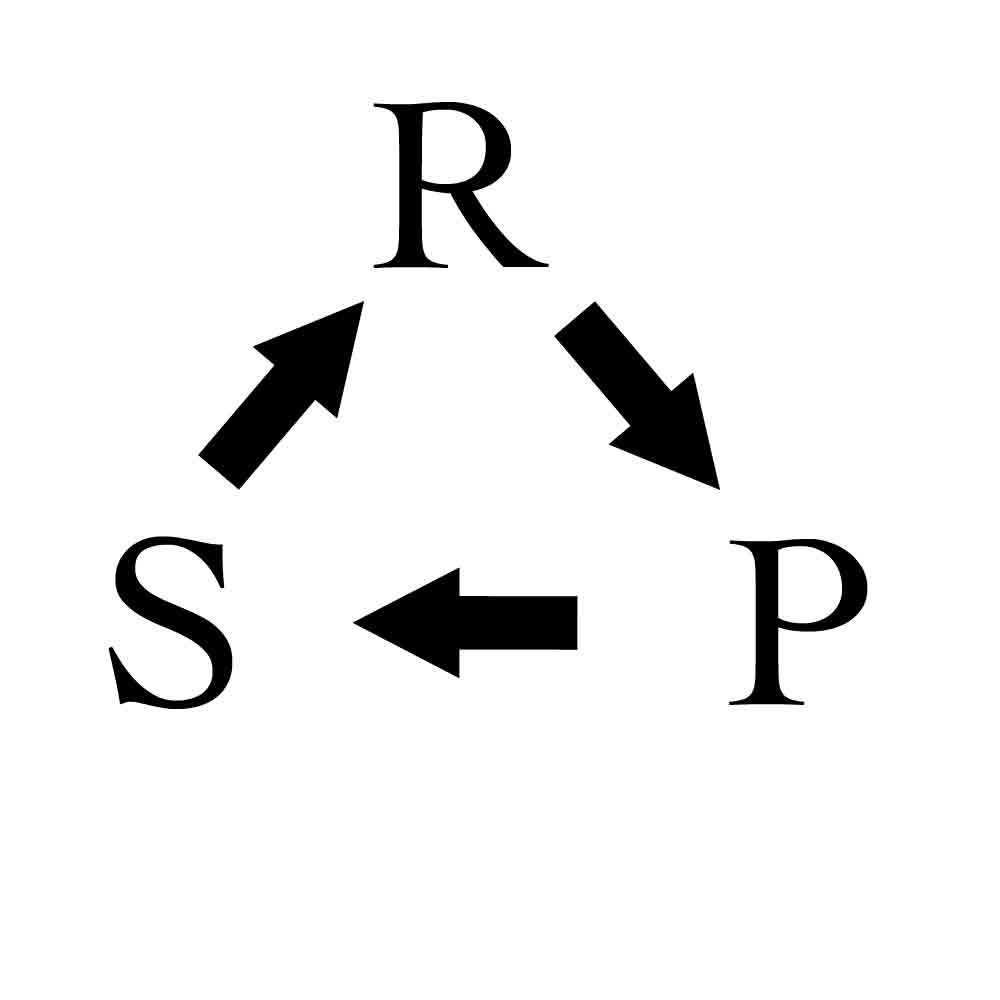
Secventa folosita de cei care pierd
Daca analizez jocul la un nivel teoretic, cel mai bun mod matematic de a juca Piatra, hartie, foarfeca este sa alegi o strategie aleatorie. Pentru ca exista 3 rezultate posibile - victoria, infrangerea si remiza - si fiecare strategie are o alta strategie pe care o poate bate. Indiferent ce strategie folosesti, cea mai buna varianta este sa alegi piatra in o treime din timp, hartie tot intr-o treime din timp si foarfeca, ati ghicit, intr-o treime din timp. Aceasta tactica are denumirea de Nash equilibrium.
Desi Nash equilibrium ar trebui sa fie cea mai buna strategie in lumea reala, Zhijian a gasit un sablon diferit cand el si cu colegii sai au studiat 72 de studenti jucand Piatra, hartie, foarfeca. Au impartit studentii in 12 grupuri a cate 6 jucatori si fiecare dintre ei a jucat 300 de runde de Piatra, hartie, foarfeca unul impotriva celuilalt. Zhijian a adaugat si o rasplata in functie de proportia castigurilor.
Cand Zhijian a verificat rezultatele, a descoperit ca studentii au ales fiecare strategie in aproape o treime din cazuri, sugerand astfel valabilitatea teoriei Nash equilibrium. Cu toate astea, a descoperit si un alt sablon neobisnuit.
Sablonul descoperit de Zhijian - castigatorii repetandu-si strategia si invinsii trecand la urmatoarea in secventa - se numeste "raspuns conditional" in teoria jocului. Cercetatorii au teoritizat ca raspunsul ar putea fi nemodificabil in creier, o intrebare pe care vor sa o studieze si cu alte experimente.
Momentan, Zhijian sugereaza ca exploatarea cunostintelor ca majoritatea oamenilor folosesc strategia conditionala rezulta in castigarea a mai multe meciuri de Piatra, hartie, foarfeca
How To Beat Anyone At Rock-Paper-Scissors, According To A Chinese Mathematician http://t.co/GTFcyQPbq3 via @BI_Science
— Angry CPU (@AngryCPU) December 7, 2014